The proposition
Have you heard this one before? Some guy called Steve comes up to you and says that he can beat roulette. All he does is keep betting on black, then double every time he loses. As long as he follows this strategy, Steve can’t lose!
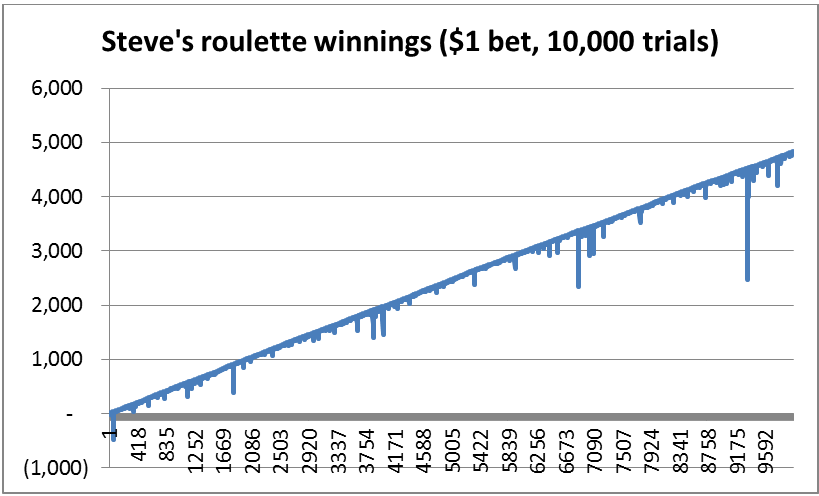
He even puts together a quick Monte Carlo simulation to prove it to you. Check out the results below:
See, there are some bumps, but in the long run, you’re guaranteed to make money! Genius! Those stupid casinos don’t stand a chance against a genius like Steve!
Starting from a $0 balance, and a $1 bet, after 10,000 rounds, Steve finishes with $4,828 in the bank.
The reality check
If beating roulette is so easy, why do casinos have it? Why aren’t statistical geniuses like Steve robbing casinos blind all the time?
Is it really this simple? You have probably guessed that it is not. But why?
Part of the answer has to do with liquidity constraints, and the other part has to do with what most people would consider to be an appropriate return for a given level of risk. Both of these things have some pretty profound implications and describe some important things about how people, firms and governments act in the real world. So, let’s get to it.
Liquidity constraints
You might have noticed one funny thing about the example above. Steve started with a zero bank balance. In the real world, casinos don’t just let you walk in with no cash in hand and start gambling. You have to have money to bet money.
Steve was also a little tricky in the way he developed his graph above. He showed you 10,000 scenarios, which sounds like it would be enough to show you a trend, but he picked one of the better rounds of 10,000 scenarios. Let me show you another few rounds of 10,000 scenarios that I just generated using Monte Carlo simulation:
In the first example above, the biggest bet Steve has to make to keep himself in business is $8,192. In the second, the biggest bet is $16,384. Has he got that sort of cash lying around? If not, is someone going to lend him that money? If not, he hasn’t got a viable business model here.
The other major constraint on Steve is the fact that tables typically have upper and lower limits on how much you can bet. I don’t hang out in casinos much, but a bit of googling makes it sound like common lower and upper limits for tables are $5 and $500, or $10 and $1000. On these sorts of tables, Steve would have maxed out and lost his shirt.
Let’s say for the sake of argument that Steve has $1,000 in his pocket that he scrimped and saved up with big dreams of hitting it rich. He has told all of his friends about his genius system, and 99 of them want to join him, all of them with $1,000 in their pockets. They quit their jobs, and take the bus down to the casino to start their new full-time jobs playing roulette. For the sake of our example, let’s say they find a casino that has a $1 minimum and some arbitrarily large upper limit on the bet at the tables. What would happen to them?
So, they all turn up at their new job, playing roulette, on Monday morning and start playing, 8 hours a day for the first week at 30 seconds per spin. Starting at $1 per bet, doubling if they don’t win, and going home if they run out of money. By Monday mid-morning the following week, Steve is still at it, and has clocked 5,000 spins. He looks around to see how everyone’s doing and is surprised to see that the 100 of them that started have been whittled down to 13, including himself.
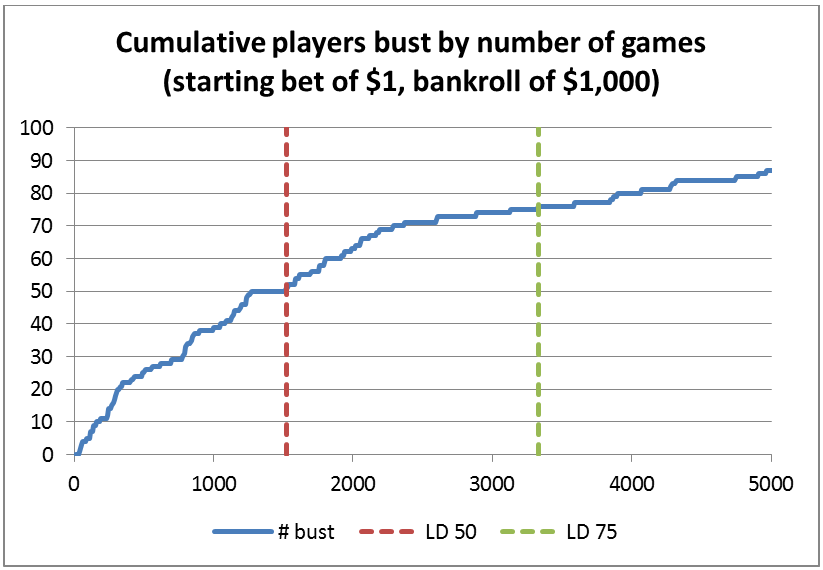
LD 50 means something like this.
In fact, half of their mates were gone by the 1,520th spin, just after lunch on the second day of their new career, and 75% were done by the 3,900th, just before close of business on the fourth day. The first of their mates to fall was done by the 31st spin.
On the first day, the 100 of them started with $100,000. After the 5,000th spin, the aggregate bank balance was $34,385, meaning they had lost $65,615 to the casino over that time.
The graph below shows the distribution of their ending bank balances.
You can see that 87 of them lost everything. A few are in the 3000s, and a few more are in the middle*.
So, what’s going on?
If you’re starting with $1000 in the bank and kicking off your betting with $1, you’ll stay solvent as long as you don’t get 10 losses in a row, or 11, 12 and so on if you’ve had some time to build up your bank with some winnings. “But”, Steve insists, “the chances of that happening are tiny. Look at my table below!”
This is true, the chances of getting 10 or 11 losses in a row are very small (1 in 692, and 1 in 1330, respectively. But, small chances have a way of adding up when you play thousands of games. Have a look at the following table that shows you your chance of a streak of X losses occurring when you play Y games. As an example, in the top left corner, you’ve got a 2.07% chance of a streak of 5 losses not occurring when you play 100 games, or a 67.64% chance of a streak of 12 losses not occurring when you play 1,000 games.
In this table, cells that are red mean that you’re highly likely to see streaks this long, yellow means you’re about 50-50, and green means you’re pretty safe.
If you’re playing with a bank of a million dollars and you play 20,000 games (about a month, full-time, by my count), you’ve got a bit over a 4% chance of losing your full million dollars… Does that sound like a safe bet to you?
So, if that’s the risk, what are the returns? For Steve and his mates, the average return they got is negative $656. So, let’s look at the guy that did the best. He came out with $3,439 in the bank, or a net gain of $2,439. Not bad for a week’s work, but he also suffered through around an 87% chance of losing that money.
That doesn’t sound like a very good deal to me.
In fact, you’d get better odds just betting the whole $1,000 on black, then, if you win, betting your $2,000 on black again. In that case, you’ll get $3,000 profit if you win, and “only” a 77% chance of losing your money. You also get to spend your week doing something more fun than staring at a roulette wheel in a soulless casino.
In summary, yes, Steve’s system can make you a small amount of money, but it carries with it an unacceptably high risk for the potential reward.
So what?
So what? Well, most of my readers probably aren’t the type to think that they can beat casinos, so why am I spending all this time debunking stupid roulette strategies that have been debunked hundreds of times**.
I generally blog about infrastructure and public sector issues, and this sort of thing has pretty profound implications for the sort of long-term ventures that governments are required to enter into as a part of their regular course of business. If a government and a private party agree to build a power plant and operate it over a 30 year period, the risk of a major earthquake occurring on any given day is very low, but the chance of one occurring over a 30 year period might be extremely high; especially in a place like Indonesia, where I live. Other low probability, high-impact events include things like currency shocks, demand shocks, civil disorder, and so on.
Arrangements like our friend Steve’s roulette strategy are what people like Nassim Nicholas Taleb calls a “fragile system.” That is, it’s a system that works, and looks great at first, because it works the vast majority of the time; but when it is tested by extreme events, it fails catastrophically.
This is also an example of something I wrote about in an early blog post, where I urge readers to balance quantitative analysis with an understanding of the real world, and I said “there’s nothing more dangerous than a genius with a model.” Not that Steve is a genius, but to someone with little understanding of statistics, he might sound like one***.
Lessons for the real world
So, what can we learn from the experience of Steve and his mates that we can apply to decision-making in business and government?
- When you build a system, don’t ignore the low probability events; especially when your system is expected to be long-lived.
- Just because something seems to be working for someone in the short-term doesn’t mean it’s a good system.
- If someone is using fancy mathematics to make an extraordinary claim, be extremely sceptical, and make sure you do your own homework and understand it before putting it into practice.
* It’s kind of interesting to look at why the ones that are in the middle are there. They aren’t there because they’re on big losing streaks, they’re there because they ran up against their minimum bank balance so couldn’t double their previous bet. The following graph shows the bank balances of two players, one that managed to avoid hitting the minimum balance, and one that hit it three times and managed to survive, although weakened.
** Most comprehensively here and here.
*** Despite being comprehensively debunked, there are plenty of clowns trying to pass themselves off as geniuses to sell their garbage systems, or encourage you to try them in their casinos. In their cases, they may well be geniuses, but their genius is in creating enticing systems to scam people rather than in advanced statistics.